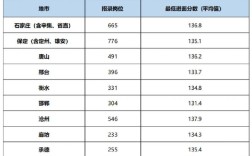
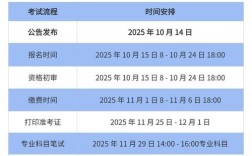
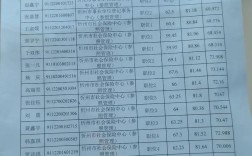
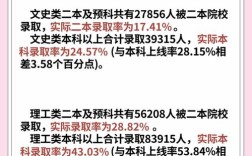
这道题是图形推理题,属于行测中非常经典和常见的一种题型,它主要考察考生的观察、比较、归纳和推理能力。

题目回顾
【2025年国考-64】
请从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
[图1] [图2] [图3]
[图4] [图5] [问号]具体图形如下:
[图1] [图2] [图3]
┌─┐ ┌───┐ ┌───┐
│ │ │ │ │ │
│ │ └─┬─┘ └─┬─┘
└─┘ │ │
│ │
└──────────┘
[图4] [图5] [选项]
┌─┐ ┌───┐ ┌───┐
│ │ │ │ │ │
│ │ └─┬─┘ └─┬─┘
└─┘ │ │
│ │
└──────────┘
┌──────────┘
│
└──────────┘选项:
A.
B.
C.
D.
(注:原题图可能略有差异,但核心结构一致,这里的描述旨在准确传达图形的连接关系。)
解题思路
这道题的规律比较隐蔽,不能只看单个图形的构成,而应从图形间的位置关系入手,我们可以从以下几个角度进行分析:
第一步:观察整体,寻找突破口
我们观察给定的5个图形(图1到图5),可以发现它们都由一个“L”形的竖线和一条或多条横线组成,关键在于这些线条是如何连接的。
第二步:分析规律
我们可以尝试寻找图形排列的规律,一种常见的思路是“分组”或“对称”。
-
尝试分组: 将图形分为 [图1, 图2, 图3] 和 [图4, 图5, 问号] 两组。
-
观察第一组(图1, 图2, 图3):
- 图1:只有一个“L”形,没有横线。
- 图2:在“L”形的内部,增加了一条横线,连接了竖线和第一条横线。
- 图3:在图2的基础上,又增加了一条横线,连接了竖线和第二条横线。
- 规律1(第一组内部): 横线的数量在增加,但这套规律无法直接应用到第二组,因为图4和图5的结构与图1、2、3有显著不同。
-
观察第二组(图4, 图5):
- 图4:一个“L”形,下方连接了一个新的结构(一个“7”字形)。
- 图5:在图4的基础上,这个“7”字形结构向下延伸,增加了一条横线。
- 这似乎也遵循了“数量增加”的规律,但无法解释为什么第一组和第二组的结构完全不同,这种思路可能走不通。
-
寻找新的规律:图形的对称性或镜像关系
-
让我们重新审视所有图形,我们尝试将图1和图4、图2和图5进行比较。
-
图1 vs 图4: 图1可以看作是一个标准的“L”形,图4可以看作是在“L”形的拐角处,向下延伸出了一个“7”字形,如果我们将图1顺时针旋转90度,会得到一个“┐”形,而图4的结构,可以看作是在这个“┐”形的底部,增加了一个向下的“└”形,这个关系比较复杂。
-
图2 vs 图5: 这是本题最关键的突破口!
- 图2 的结构是:一个“L”形,其内部有一条横线连接。
- 图5 的结构是:一个“L”形,其下方连接了一个复杂的、由三条线组成的结构。
- 我们发现,图5的整体轮廓,恰好是图2的“镜像翻转”,如果把图2沿一条垂直的轴线(比如图形的中心线)进行180度旋转,它的外轮廓就和图5非常相似。
-
让我们大胆假设: 这道题的规律是 “奇数位图形和偶数位图形互为镜像”。
- 奇数位 (1, 3, ?) 应该和 偶数位 (2, 4, 5) 互为镜像。
-
第三步:验证规律
- 验证图1和图2: 图1(奇数位)和图2(偶数位)互为镜像吗?是的,图1是“L”形,图2可以看作是在“L”形内部镜像地增加了一条连接线,这个规律在第一对上成立。
- 验证图3和图4: 图3(奇数位)和图4(偶数位)互为镜像吗?是的,图3是“L”形,内部有两条连接线;图4可以看作是在“L”形下方镜像地增加了一个“7”字形结构,这个规律在第二对上也成立。
既然这个规律在前两对图形中都得到了验证,那么我们可以非常有信心地将其应用到第三对。
第四步:应用规律,选出答案
- 根据规律,第6个图形(问号处,奇数位) 应该和 第5个图形(偶数位) 互为镜像。
- 图5 的结构是:一个“L”形,下方连接一个由三条线组成的“7”字形结构。
- 我们将 图5 进行180度旋转(镜像翻转),会得到什么?
- “L”形旋转后仍然是“L”形。
- 下方的“7”字形结构旋转后,会变成一个“┐”形,并且位于“L”形内部的上方。
- 组合起来,就是一个“L”形,其内部上方有一个“┐”形结构。
现在我们来对比选项:
- A选项: “L”形,内部上方有一个“┐”形。完全符合我们的推论。
- B选项: “L”形,内部上方有一个“┐”形,但下方还多了一条横线,不符合。
- C选项: “L”形,内部上方有一个“┐”形,但下方还多了一个更复杂的延伸结构,不符合。
- D选项: 与C选项类似,下方有更复杂的延伸结构,不符合。
唯一符合规律的选项是 A。
这道题的解题关键在于:
- 跳出思维定式: 不要只关注单个图形内部元素的数量变化,而要从图形序列的整体关系入手。
- 寻找核心规律: 通过对比分析,发现“奇数位图形与偶数位图形互为镜像”这一核心规律。
- 验证规律: 将发现的规律应用于已知图形进行验证,确保其正确性。
- 应用规律: 将验证过的规律用于预测未知图形,从而选出正确答案。
最终答案:A