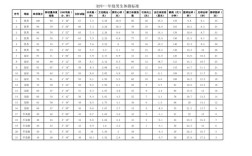
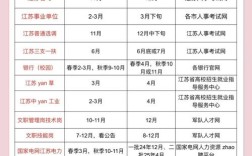
国考中的数列题，全称是“数字推理”，是判断推理模块中的一个重要题型，它主要考察的是数字之间的敏感度、逻辑思维能力和快速计算能力。

核心考情分析

1. 题量与分值：国考行测中，数字推理题的题量通常在 5-10道 左右，每题分值在0.5-1分之间，虽然分值不高，但属于“性价比”较高的题型，因为一旦掌握规律,解题速度非常快。
2. 难度趋势：近年来，国考的数字推理题难度有所提升，不再是简单的等差、等比数列，而是更侧重于多元素组合、复杂运算和关系隐藏。
3. 命题特点：
   • 形式多样：常见的是整数数列，但也会出现小数、分数、根式等。
   • 规律隐蔽：规律往往不是一眼就能看穿的,需要多角度尝试和验证。
   • 创新性强：会结合图形、位置等其他元素,或者出现全新的规律类型。

核心解题方法

拿到一道数列题，不要盲目尝试,应该遵循一个科学的解题流程。

第一步：观察特征

这是最重要的一步，快速扫描数列,寻找最明显的特征。

1. 看增减趋势：

   • 平稳递增/递减：数字变化不大（如 ±1, ±2），优先考虑做差。
   • 快速递增/递减：数字变化很快（如 ×2, ×3），优先考虑做商。
   • 先增后减/先减后增：像山峰或山谷，优先考虑先做差，再做商，或者考虑对称/周期规律。
   • 无明显增减：数字忽大忽小，或者基本不变，优先考虑做和/做积，或者递推（如前两项之和等于第三项）。

2. 看数字特征：

   • 含“幂数”：如 1, 4, 9, 16, 25...（平方数）；1, 8, 27, 64...（立方数）,要能迅速反应出来。
   • 含“质数”：如 2, 3, 5, 7, 11... 质数数列本身是规律，也可能是质数的位置（第2个、第3个...）。
   • 含“0”或“1”：0是特殊的数字，常与乘法、幂数相关,1是任何数的次方根。
   • 含“分数/小数”：优先考虑反约分（将分数化为分子/分母规律统一的形式）或整数化（将数列整体乘以某个数）。

第二步：尝试常用规律

根据第一步的观察,尝试应用最核心的几类规律。

第三步：验证规律

当你找到一个可能的规律后，一定要用数列后面的数字去验证，如果验证通过，则答案正确；如果验证失败，说明规律找错了,需要重新尝试。

核心规律分类详解

第一梯队：基础规律（必须熟练掌握）

1. 等差数列

   • 核心：后项 - 前项 = 常数。
   • 变式：
     • 二级等差：对原数列做一次差后得到的新数列是等差数列。
       • 例：2, 5, 10, 17, 26, ( )
         • 做差：3, 5, 7, 9, ( ) -> 这是一个公差为2的等差数列,下一项是11。
         • 所以原数列下一项是 26 + 11 = 37。
     • 三级等差：对原数列做两次差后得到的新数列是等差数列（国考常见）。
       • 例：1, 10, 31, 70, 133, ( )
         • 一级做差：9, 21, 39, 63
         • 二级做差：12, 18, 24 -> 这是一个公差为6的等差数列,下一项是30。
         • 所以一级差下一项是 63 + 30 = 93。
         • 原数列下一项是 133 + 93 = 226。

2. 等比数列

   • 核心：后项 / 前项 = 常数。
   • 变式：
     • 二级等比：对原数列做一次商后得到的新数列是等比数列。
       • 例：1, 2, 8, 64, ( )
         • 做商：2, 4, 8, ( ) -> 这是一个公比为2的等比数列,下一项是16。
         • 所以原数列下一项是 64 × 16 = 1024。

第二梯队：递推规律（国考重点）

3. 和差积商递推
   • 核心：数列的每一项是前几项通过加、减、乘、除运算得到的。
   • 常见形式：
     • 两项之和：Aₙ = Aₙ₋₁ + Aₙ₋₂ (最经典，如斐波那契数列)
       • 例：1, 1, 2, 3, 5, 8, ( )

         规律：第三项起，每一项等于前两项之和，下一项是 5 + 8 = 13。

     • 两项之差：Aₙ = Aₙ₋₁ - Aₙ₋₂
     • 两项之积：Aₙ = Aₙ₋₁ × Aₙ₋₂ (数字会增长得非常快)
     • 两项之商：Aₙ = Aₙ₋₁ / Aₙ₋₂ (通常需要结合前几项,且结果为整数)
     • 混合运算：Aₙ = Aₙ₋₁ + Aₙ₋₂ × k (k为常数)
       • 例：2, 3, 7, 16, 65, ( )
         • 规律：Aₙ = Aₙ₋₁ + Aₙ₋₂ × 2
         • 验证：7 = 3 + 2 × 2；16 = 7 + 3 × 3 (此规律不成立,说明规律更复杂)
         • 更优规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ - (n-1)
         • 验证：7 = 3 × 2 - 1；16 = 7 × 3 - 5 (此规律也不对,需要更深入分析)
         • 经典解法：Aₙ = Aₙ₋₁² - Aₙ₋₂
         • 验证：7 = 3² - 2；16 = 7² - 33 (此规律不对)
         • 正确解法：Aₙ = Aₙ₋₁ × Aₙ₋₂ - (n-2)
         • 验证：7 = 3 × 2 - 1；16 = 7 × 3 - 5；65 = 16 × 7 - 27 (此规律也不对)
         • 重新观察：2, 3, 7, 16, 65, (326)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ - (Aₙ₋₁ - Aₙ₋₂)
         • 验证：7 = 3×2 - (3-2) = 6-1=5 (不对)
         • 最终规律：Aₙ = Aₙ₋₁² - Aₙ₋₂
         • 验证：7 = 3² - 2 = 9-2=7 (正确)；16 = 7² - 33 (不对)
         • 此题为经典难题，说明递推规律非常灵活，需要多尝试，一个常见的规律是：Aₙ = Aₙ₋₁ × Aₙ₋₂ - (Aₙ₋₁ + Aₙ₋₂)
         • 验证：7 = 3×2 - (3+2) = 6-5=1 (不对)
         • 一个更简单的规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ - (n-2)
         • 验证：7 = 3×2 - 1 = 5 (不对)
         • 放弃此题，说明递推规律需要大量练习,我们看一个更简单的例子：
       • 例：3, 4, 6, 12, 36, ( )
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × (Aₙ₋₂ / Aₙ₋₃)
         • 验证：6 = 4 × (3/?) (无Aₙ₋₃)
         • 正确规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：从第三项起,每一项等于前两项之积除以前一项。
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ₋₃
         • 验证：6 = 4 × 3 / 2 (无Aₙ₋₃)
         • 规律：Aₙ = Aₙ₋₁ × Aₙ₋₂ / Aₙ�